ความมหัศจรรย์ของ ตัวเลข Fibonacci ที่มาของอินดิเคเตอร์ Fibonacci Retracement ซึ่งจัดได้ว่า Fibonacci Retracement เป็นหนึ่งในอินดิเคเตอร์ที่ได้รับความนิยมมากที่สุดในวงการเทรดเดอร์
Fibonacci คืออะไร
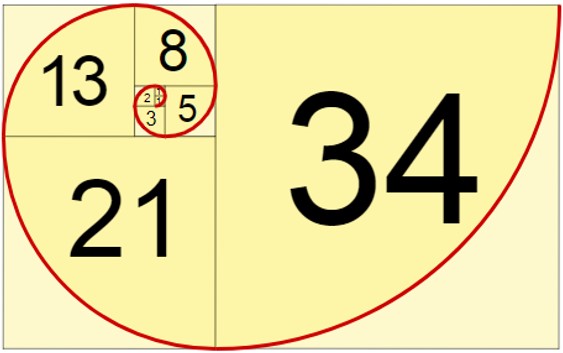
Fibonacci หรือที่รู้จักในชื่อ Leonardo Pisano เป็นนักคณิตศาสตร์ชาวอิตาลีผู้ค้นพบลำดับตัวเลขที่มีความพิเศษ ที่เรียกว่า “ลำดับฟีโบนัชชี” ซึ่งเป็นลำดับตัวเลขที่เกิดจากการนำตัวเลขสองตัวก่อนหน้ามาบวกกัน เช่น 0, 1, 1, 2, 3, 5, 8, 13, 21, 34… ความพิเศษของลำดับนี้คือเมื่อนำตัวเลขในลำดับมาหารกัน จะได้ค่าประมาณ 1.618 หรือที่เรียกว่า “อัตราส่วนทองคำ” ซึ่งพบได้ในธรรมชาติและศิลปะมากมาย รวมถึงในการวิเคราะห์ทางเทคนิคของตลาดการเงิน
Fibonacci มีกี่ชนิด
Fibonacci ที่ใช้ในการวิเคราะห์ทางเทคนิคมีหลายรูปแบบ แต่ละแบบมีจุดประสงค์การใช้งานที่แตกต่างกัน ดังนี้
- Fibonacci Retracement : ใช้หาจุดแนวรับแนวต้านในแนวราบ โดยแบ่งระดับเป็น 23.6%, 38.2%, 50%, 61.8% และ 100%
- Fibonacci Extension : ใช้คาดการณ์เป้าหมายราคาที่จะวิ่งต่อไป มักใช้ระดับ 127.2%, 161.8%, 261.8%
- Fibonacci Time Zones : ใช้คาดการณ์จุดเวลาที่ราคาอาจเกิดการเปลี่ยนแปลงทิศทาง
- Fibonacci Arcs : แสดงความสัมพันธ์ระหว่างราคาและเวลาในรูปแบบวงโค้ง
- Fibonacci Fan : ใช้วิเคราะห์แนวโน้มราคาในอนาคตโดยใช้เส้นพัดที่ทำมุมต่างกัน
ทำไมต้องใช้ Fibonacci ในการเทรด
Fibonacci เป็นเครื่องมือที่มีประสิทธิภาพในการวิเคราะห์ทางเทคนิค เนื่องจากตัวเลขและอัตราส่วนของ Fibonacci มีความสัมพันธ์กับพฤติกรรมราคาในตลาดการเงิน โดยเฉพาะในการหาจุดกลับตัวของราคา เนื่องจากนักลงทุนจำนวนมากทั่วโลกใช้เครื่องมือนี้ในการตัดสินใจซื้อขาย จึงทำให้เกิดการทำนายตัวเองและกลายเป็นจุดสำคัญในการเทรด
นอกจากนี้ Fibonacci ยังช่วยในการวางแผนการเทรดอย่างเป็นระบบ ทั้งในการกำหนดจุดเข้าซื้อขาย จุดทำกำไร และจุดตัดขาดทุน โดยเฉพาะเมื่อใช้ร่วมกับเครื่องมือวิเคราะห์ทางเทคนิคอื่น ๆ เช่น แนวโน้ม แท่งเทียน และตัวบ่งชี้ต่าง ๆ ทำให้การวิเคราะห์มีความแม่นยำมากขึ้น
ความมหัศจรรย์ของ ตัวเลข Fibonacci
เลขฟีโบนัชชี เป็นตัวเลขอนุกรมหรือลำดับที่เรียงกัน และก็เรียงกันอย่างมีแบบแผน อนุกรมดังกล่าวค้นพบโดยนักคณิตศาสตร์ชาวอิตาลีนามว่า Leonardo Pisano “Bigollo” หรือรู้จักกันกว้างขวางในนามว่า Fibonacci อันเป็นชื่อของเลขอนุกรมนี้นี่เอง
เหตุผลสำคัญที่ทำให้ลำดับฟีโบนักชีเป็นที่สนใจของคนทั่วไป เป็นเพราะมีการค้นพบความสอดคล้องอย่างลงตัวมากมายของลำดับนี้กับปรากฏการณ์ในธรรมชาติ เช่น เกลียวตาสับปะรด เกลียวเกสรดอกทานตะวัน หรือเกลียวโคนต้นสน ซึ่งเมื่อนับจำนวนเกลียวเวียนซ้ายและเวียนขวาจะไม่เท่ากัน แต่กลับไปเหมือนจำนวนคู่หนึ่งที่อยู่ติดกันในลำดับฟีโบนักชี
นอกจากนี้ยังพบความสัมพันธ์กับสิ่งต่าง ๆ รอบตัวอีกมากมาย เช่น สัดส่วนในงานออกแบบสถาปัตยกรรม งานด้านดนตรี เปลือกหอยบางประเภท สัดส่วนของส่วนต่าง ๆ ในร่างกายมนุษย์และสัตว์ และนอกจากนี้ยังมีความสำคัญในตลาดการเงินอีกด้วย ในปัจจุบันนี้ก็มีเทรดเดอร์จำนวนมากที่ใช้อัตราส่วนฟีโบนัชชีในการคำนวณแนวรับและแนวต้าน เพื่อให้แต่ละการเทรดนั้นมีประสิทธิภาพมากที่สุด
เกร็ดความรู้
วันที่ 23 พฤศจิกายน ของทุกปีเป็นถือว่าเป็น “วันฟีโบนัชชี หรือ Fibonacci Day” ตั้งขึ้นเพื่อเป็นเกียรติแด่ Leonardo Bonacci ผู้ค้นพบ “ลำดับฟีโบนัชชี”
ความมหัสจรรย์ของลำดับเลขฟีโบนักชี
ตัวเลขลำดับ Fibonacci numbers
จำนวนฟีโบนัชชี หมายถึง จำนวนต่าง ๆ ที่อยู่ในลำดับดังนี้ 0,1,1,2,3,5,8,13,21,34, 55… โดยลำดับสองจำนวนแรกเป็น 0 และ 1 ส่วนจำนวนถัดไปจะมีค่าเป็นผลบวกของจำนวนก่อนหน้า
เริ่มจาก 1+1 =2 ,1+2 =3, 2+3 =5, 3+5=8,5+8=13,8+13=21,13+21=34 เป็นอย่างนี้เรื่อยไป
ตัวเลขเหล่านี้เราเรียกมันว่า เลขฟีโบนักชี เมื่อเรานำตัวเลขเหล่านี้มาบวกกับตัวที่อยู่ติดกัน จะได้เลขฟีโบนักชีตัวที่อยู่ถัดไป เป็นลำดับอนุกรมดังนี้ 1, 1, 2, 3, 5, 8,13, 21, 34, 55, 89, 144 ,233 ,377 ,610, 987 ,1597 ,2584………
หากนำตัวเลขลำดับฟีโบนักชีมายกกำลัง 2
| เลขฟีโบนักชียกกำลัง2 | 1(2) | 1(2) | 2(2) | 3(2) | 5(2) | 8(2) | 13(2) | 21(2) | 34(2) |
| สิ่งที่ได้คือ | 1 | 1 | 4 | 9 | 25 | 64 | 169 | 441 | 1156 |
เป็นแบบนี้ต่อไปเรื่อย ๆ
แล้วหากเรานำผลลัพธ์ของตัวเลขยกกำลังสอง มาบวกกัน จะได้สิ่งที่น่าสนใจต่อมาคือ
1 1 4 9 25 64 169 441 1156 3025
1 + 1 = 2 , 1 + 4 = 5 , 4 + 9 = 13 , 9 + 25 = 34,25+64=89 เป็นอย่างนี้เรื่อยไป
เมื่อนำผลลัพธ์ของตัวเลขยกกำลังสอง มาเปรียบเทียบลำดับอนุกรมฟีโบนัชชี 1, 1, 2, 3, 5, 8,13, 21, 34, 55, 89,…
ถ้าเราบวกตัวเลขลำดับเหล่านี้ เข้าด้วยกัน จะพบว่า
1 1 4 9 25 64 169 441 1156 3025
1 + 1 + 4 = 6
1 + 1 + 4 + 9 = 15
1 + 1 + 4 + 9 + 25 = 40
1 + 1 + 4 + 9 + 25 + 64 = 104
6 , 15 , 40 , 104…. ไม่ใช่จำนวนฟิโบนัชชี แต่เราพบว่าในจำนวนเหล่านี้ เกิดจากการการคูณตัวเลขของเลขจำนวนฟิโบนัชชี ดังนี้
1 + 1 + 4 = 6 = 2 X 3
1 + 1 + 4 + 9 = 15 = 3 X 5
1 + 1 + 4 + 9 + 25 = 50 = 5 X 8
1 + 1 + 4 + 9 + 25 + 64 = 104 = 8 X 13
1 + 1 + 4 + 9 + 25 + 64 + 169 = 273 = 13 X 21
1 + 1 + 4 + 9 + 25 + 64 + 169 + 441 = 714 = 21 X 34
1 + 1 + 4 + 9 + 25 + 64 + 169 + 441 + 1156 = 1870 = 34 X 55
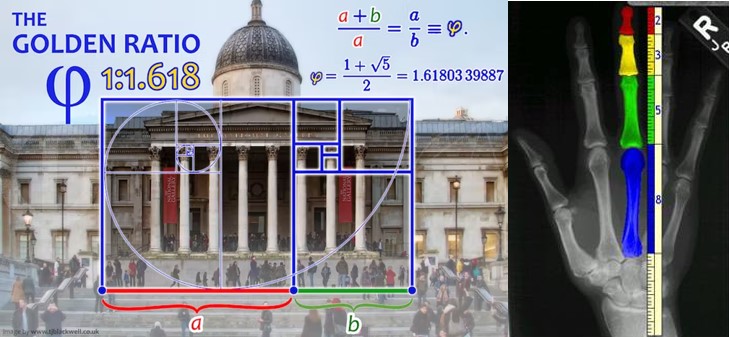
จากความมหัศจรรย์ของจำนวนตัวเลขเหล่านี้ ที่มีความสอดคล้องและเกี่ยวพันกันกับตัวเลขค่าหนึ่งที่เรียกว่า ฟี Phi (φ) หรือค่าตัวเลขคงที่ 1.618
2 X 3 3 หารด้วย 2 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.5
3 X 5 5 หารด้วย 3 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.666
5 X 8 8 หารด้วย 5 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.6
8 X 13 13 หารด้วย 8 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.625
13 X 21 21 หารด้วย 13 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.615
21 X 34 34 หารด้วย 21 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.619
34 X 55 55 หารด้วย 34 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.617
ทุกจำนวนเป็นตัวเลขฟีโบนักชี ถ้าเอาตัวเลขฟีโบนักชีตัวหนึ่งมาหารด้วยตัวเลขฟีโบนักชีลำดับก่อนหน้าจะได้ผลหารใกล้เคียงกับค่า Phi หรือ 1.618 เสมอ
Phi (φ) สี่เหลี่ยมผืนผ้าและอัตราส่วนทองคำ (Phi and Golden ratio)
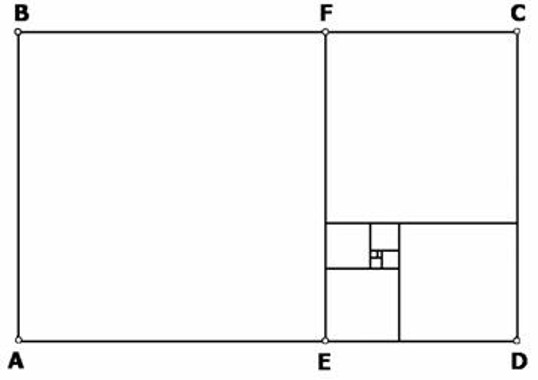
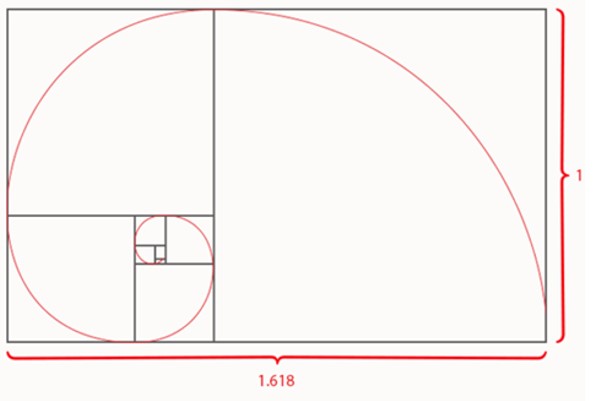
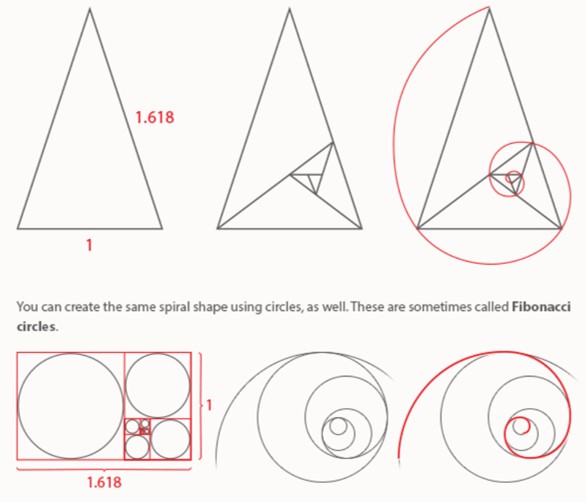
ความสัมพันธ์ของกับการนำเลขฟีโบนักชีมาสร้างเป็นสี่เหลี่ยมเพื่อหาค่าพื้นที่ดังภาพ ทำให้เกิดความสัมพันธ์หนึ่ง ที่เรียกว่า อัตราส่วนทองคำ
Phi and Golden ratio คือ สี่เหลียมผืนผ้าที่มีอัตราส่วนด้านยาวต่อด้านสั้นเท่ากับอัตราส่วนทองคำ หรือ phi นั่นเอง ความพิเศษของสี่เหลี่ยมทองคำก็คือถ้าเราแบ่งสี่เหลี่ยมผืนผ้าทองคำออกเป็นสองส่วน โดยส่วนแรกเป็นสี่เหลี่ยมจัตุรัส และส่วนที่สองเป็นสี่เหลี่ยมผืนผ้าก็จะพบว่าสี่เหลี่ยมผืนผ้าอันเล็ก ที่เกิดขึ้นมาใหม่ก็ยังคงเป็นสี่เหลี่ยมผืนผ้าทองคำเช่นเดียวกัน ซึ่งถ้าเรายังแบ่งสี่เหลี่ยมผืนผ้าทองคำ ที่เกิดขึ้นใหม่ด้วยวิธีการเดียวกันนี้ ก็จะได้สี่เหลี่ยมจัตุรัสและสี่เหลี่ยมผืนผ้าทองคำ ที่มีขนาดเล็กลงไปเรื่อย ๆ ซ้ำไปซ้ำมาจนไม่รู้จบ
Phi มีบทบาทในการเป็นรากฐานที่สำคัญให้กับธรรมชาติ คน สัตว์ พืช หรือแม้แต่อะตอม ซึ่งต่างก็มีสัดส่วนที่ตรงกับอัตราส่วนของ Phi ต่อ 1 อย่างน่าอัศจรรย์!
จึงทำให้การปรากฏอยู่ ของตัวเลข Phi ในธรรมชาติ มีมากเกินกว่าที่จะเป็นการบังเอิญ จนราวกับว่าตัวเลข Phi ถูกสร้างขึ้นโดยพระเจ้า
จนถึงทุกวันนี้ได้มีการค้นพบว่า Phi เข้าไปเกี่ยวข้องกับธรรมชาติ และสิ่งต่าง ๆ อย่างมากมาย เช่น ศาสตร์สัญลักษณ์ในวงการศิลปะ, สถาปัตยกรรม เช่น พีระมิดอียิปต์, ดนตรี, เกลียวสับปะรด, หลุมดำ, ซุปเปอร์โนวา และทฤษฎี string ฯลฯ ตัวอย่างของสิ่งต่าง ๆ ที่เกี่ยวข้องกับ Phi มีดังนี้
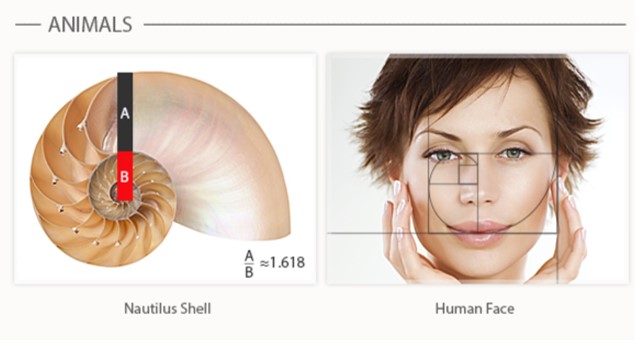
- อัตราส่วนระหว่างเส้นผ่านศูนย์กลางของเกลียวรอบเปลือกหอยนอติลุส
- อัตราส่วนเส้นผ่านศูนย์กลางของวงขดเกลียวของเมล็ดทานตะวันแต่ละวงเทียบกับวงถัดไป
- อัตราส่วนของสัดส่วนหน่วยโครงสร้างร่างกายมนุษย์ เช่นความยาวของกระดูกนิ้วมือ
- งานศิลปะและสถาปัตยกรรมของจำนวนมากมาย
การใช้ฟีโบนัชชีในกราฟฟิกดีไซน์
เพื่อให้เข้าใจลำดับฟีโบนัชชีมากขึ้น เราจะมาทำความเข้าใจในทฤษฎีต่างๆที่ Leonardo ได้ค้นพบและเผยแพร่
- ทฤษฎีพันธุ์กระต่าย ตัวเลขฟีโบนัชชี กับจำนวนคู่ของกระต่าย
- ทฤษฎีตัวเลขฟีโบนัชชี กับเกลียวเกสรดอกดอกทานตะวัน
ทฤษฎีพันธุ์กระต่าย ตัวเลขฟีโบนัชชี กับจำนวนคู่ของกระต่าย
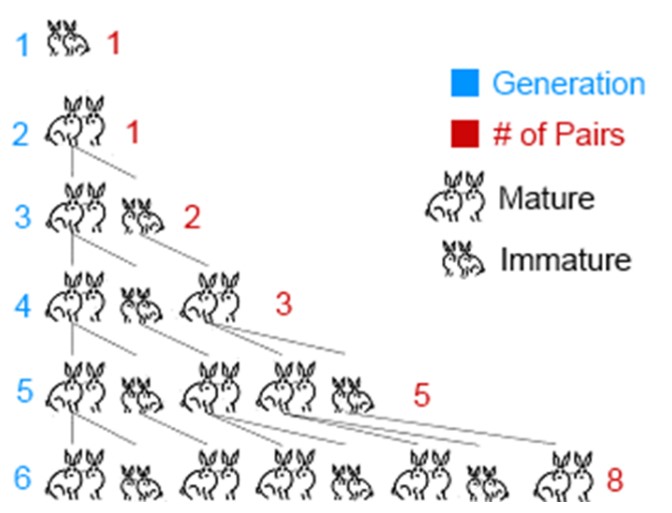
คำถามข้อนี้มีอยู่ว่า “ถ้ากระต่ายหนึ่งคู่ออกลูกได้เดือนละคู่ และลูกกระต่ายสามารถแพร่พันธ์ต่อได้ในเดือนที่สองหลังเกิด ผ่านไปหนึ่งปีจะมีกระต่ายกี่คู่?”
จากโจทย์สามารถคำนวณได้ว่า
- เดือนที่ 1 จะมีกระต่ายหนึ่งคู่ คือ คู่แรกคู่เดียว
- เดือนที่ 2 กระต่าย 1 คู่จะเพิ่มเป็น 2 คู่
- เดือนที่ 3 กระต่าย 2 คู่จะเพิ่มเป็น 3 คู่
- เดือนที่ 4 กระต่าย 3 คู่จะเพิ่มเป็น 5 คู่
- เดือนที่ 5 กระต่าย 5 คู่จะเพิ่มเป็น 8 คู่
- เดือนที่ 6 กระต่าย 8 คู่จะเพิ่มเป็น 13 คู่
- เดือนที่ 7 กระต่าย 13 คู่จะเพิ่มเป็น 21 คู่
- เดือนที่ 8 กระต่าย 21 คู่จะเพิ่มเป็น 34 คู่
- เดือนที่ 9 กระต่าย 34 คู่จะเพิ่มเป็น 55 คู่
- เดือนที่ 10 กระต่าย 55 คู่จะเพิ่มเป็น 89 คู่
- เดือนที่ 11 กระต่าย 89 คู่จะเพิ่มเป็น 144 คู่
- เดือนที่ 12 กระต่าย 144 คู่จะเพิ่มเป็น 233 คู่
จำนวนคู่ของกระต่ายแต่ละเดือนคือ 1,2,3,5,8,13 ซึ่งเห็นได้ว่านอกจากเลขสองลำดับแรกแล้ว เลขลำดับถัดมาต่างเป็นผลบวกของเลขสองลำดับก่อนหน้านั้นทั้งสิ้น จากลำดับดังกล่าวเราสามารถเรียงลำดับจำนวนคู่ของกระต่ายในแต่ละเดือนเป็น 1,2,3,5,8,13,21,34,55,89,144,233 ดังนั้นในหนึ่งปีจะมีกระต่าย 233 คู่ ดังนั้นผู้คนจึงตั้งชื่อลำดับตัวเลขดังกล่าวว่า “จำนวนฟีโบนัชชี”
การแก้โจทย์คณิตศาสตร์ในครั้งนี้ทำให้ตัว Leonardo Pisano “Bigollo” ได้รับการยอมรับและมีชื่อเสียงอยู่ในระดับหนึ่งในยุคนั้น
ทฤษฎีตัวเลขฟีโบนัชชี กับเกลียวเกสรดอกดอกทานตะวัน
จากการศึกษาพบว่าดอกไม้เกือบทุกชนิดจะมีจำนวนกลีบดอกเท่ากับลำดับเลขฟีโบนักชี และดอกทานตะวันก็เป็นหนึ่งในการศึกษาที่ Leonardo Pisano “Bigollo” ได้คนพบการจัดเรียงตัวเป็นเกลียว แต่ละเกลียวจะตรงกับเลขฟีโบนักชี จำนวนเมล็ดที่อยู่ในเกลียว ที่หมุนตามเข็มนาฬิกามีอัตราส่วนเท่ากับอัตราส่วนทองคำ “phi”
ลำดับฟีโบนัชชีกับการเทรด
ทั้งนี้ทั้งนั้นความมหัศจรรย์ของสัดส่วนดังกล่าวที่เกิดขึ้นทำให้นักเทคนิคนำไปประยุกต์ใช้ในการเทรด โดยสามารถใช้ Fibo Retracement เป็นเครื่องมือในการหา
- แนวรับของราคา
- แนวต้านของราคา
เพื่อดูว่าเราจะใช้ ลำดับฟีโบนัชชีในการหาจุดเข้า Buy หรือเข้า Sell เพื่อให้การเทรดเป็นไปอย่างคุณภาพ เพิ่มอัตตราการชนะ
จากตัวอย่าง เราสามารถเห็นราคาตามระดับฟีโบนัชชีได้อย่างชัดเจน และการเทรดโดยใช้เครื่องมือนี้ ทำให้เราสามารถคาดการณ์แนวโน้มของราคาได้
การใช้เครื่องมือ Fibonacci retracements เป็นการวัดรอบการแกว่งตัวของราคาเพื่อหาจุดกลับตัวของรอบ ซึ่งสามารถใช้จับจังหวะในการซื้อขายได้เป็นอย่างดี และยิ่งถ้าไปใช้ประกอบกับเครื่องมืออื่นอย่างเช่น การดู Price action, Indicator ต่าง ๆ เป็นต้น ก็จะยิ่งทวีความมีประสิทธิภาพในการเทรดขึ้นไปอีกด้วยเช่นเดียวกัน
Source
- https://www.linkedin.com/pulse/fibonacci-spiral-nature-utkarsh-gaikwad/
- https://www.moneymuseum.com/en/focus/crisis/fibonacci-and-the-sunflower-307?slbox=true
- https://www.youtube.com/watch?v=2tv6Ej6JVho
- https://r-knott.surrey.ac.uk/Fibonacci/fibnat.html
- https://www.ted.com/talks/arthur_benjamin_the_magic_of_fibonacci_numbers?language=th
- https://clevelanddesign.com/insights/the-nature-of-design-the-fibonacci-sequence-and-the-golden-ratio/
- https://www.forex.academy/62-using-fibonacci-retracements-to-enter-a-trade/
- https://school.stockcharts.com/doku.php?id=chart_analysis:fibonacci_retracemen
Author: